Akida user guide
Overview
Like many other machine learning frameworks, the core data structures of Akida are layers and models, and users familiar with Keras, Tensorflow or Pytorch should be on familiar ground.
The main difference between Akida and other machine learning networks is that inputs and weights are integers and it only performs integer operations, so that it can further reduce the power consumption and memory footprint. Since quantization and ReLU activation functions lead to a substantial sparsity, Akida takes advantage of this by implementing operations in biologically inspired event-based calculations. However, to simplify the user experience, the model weights and the inputs are represented as integer tensors (Numpy arrays), similar to what you would see in other machine learning frameworks.
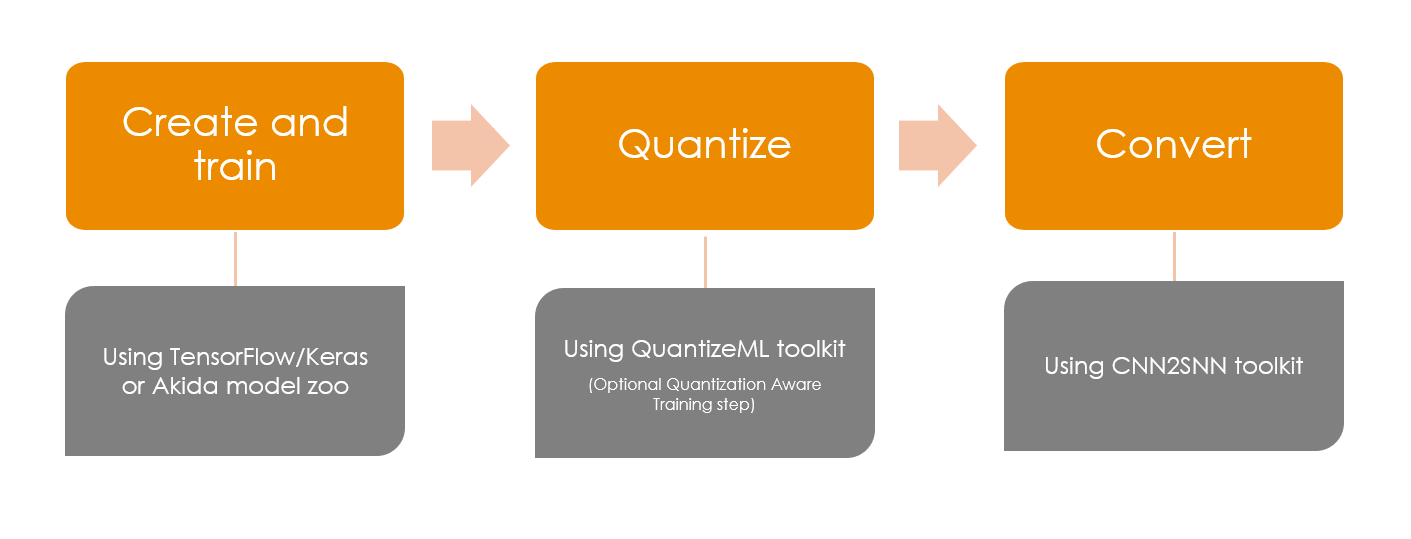
Going from the standard deep learning world to Akida world is done by following simple steps:
build a model using Keras or optionally using a model from the Brainchip zoo
quantize the model using the QuantizeML toolkit
convert the model to Akida using the CNN2SNN toolkit
Akida workflow
A practical example of the overall flow is given in the examples section, see the workflow tutorial.
Programming interface
The Akida Model
Similar to other deep learning frameworks, Akida offers a Model grouping layers into an object with inference features.
The Model object has basic features such as:
summary() method that prints a description of the model architecture.
save() method that needs a path for the model and that allows saving to disk for future use. The model will be saved as a file with an
.fbzextension. A saved model can be reloaded using theModelobject constructor with the full path of the saved file as a string argument. This will automatically load the model weights.from akida import Model model.save("my_model.fbz") loaded_model = Model("my_model.fbz")
forward method to generate the outputs for a specific set of inputs.
import numpy as np # Prepare one sample input_shape = (1,) + tuple(model.input_shape) inputs = np.ones(input_shape, dtype=np.uint8) # Inference outputs = model.forward(inputs)
predict method is very similar to the forward method, but is specifically designed to replicate the float outputs of a converted CNN.
statistics member provides relevant inference statistics.
Akida layers
The sections below list the available layers for Akida 1.0 and Akida 2.0. Those layers are obtained from converting a quantized model to Akida and are thus automatically defined during conversion. Akida layers only perform integer operations using 8-bit or 4-bit quantized inputs and weights. The exception is FullyConnected layers performing edge learning, where both inputs and weights are 1-bit.
Akida 1.0 layers
Akida 2.0 layers
Model Hardware Mapping
By default, Akida models are implicitly mapped on a software backend: in other words, their inference is computed on the host CPU.
Devices
In order to perform model inference on hardware, the corresponding Model object must first be
mapped on a specific Device.
The Akida Device represents a device object that holds a version and the hardware topology of the
mesh. The main properties of such object are:
its hardware version,
the description of its mesh of processing nodes.
Discovering Hardware Devices
The list of hardware devices detected on a specific host is available using the devices() method.
from akida import devices
device = devices()[0]
print(device.version)
It is also possible to list the available devices using a command in a terminal:
akida devices
Virtual Devices
Most of the time, Device objects are real hardware devices, but virtual devices can also be
created to allow the mapping of a Model on a host that is not connected to a hardware device.
It is possible to build a virtual device for known hardware devices, by calling functions AKD1000() and TwoNodesIP().
Model mapping
Mapping a model on a specific device is as simple as calling the Model
.map() method.
model.map(device)
When mapping a model on a device, if the Model is too big to fit on the device or contains layers that are not hardware compatible, it will be split into multiple parts called “sequences”.
The number of sequences, program size for each and how they are mapped are included in
the Model .summary() output after it
has been mapped on a device.
Advanced Mapping Details and Hardware Devices Usage
When Model .map() results in more than
one hardware sequence, on inference each sequence will be chain loaded onto the device to process a
given input. Sequences can be obtained using the Model
.sequences() property, that will return
a list of sequence objects. The program used to load one sequence can be obtained programmatically.
model.map(device)
print(len(model.sequences))
# Assume there is at least one sequence.
sequence = model.sequences[0]
# Check program size
print(len(sequence.program))
Once the model has been mapped, the sequences mapped in the Hardware run on the device, and the sequences mapped in the Software run on the CPU.
Note
Where mapping to a single on-hardware sequence is necessary, one can force an exception to be
raised if that fails by setting the hw_only parameter to True (default False). See the
.map() method API for more details.
model.map(device, hw_only=True)
By default, the mapping uses the MapMode.AllNps mode that targets a higher throughput, lower latency, and better NP concurrent utilization but an optimal mapping depends on the system characteristics. The other modes MapMode.HwPr and MapMode.Minimal will respectively leverage the NP concurrent utilization along with partial reconfiguration (multipass) and use as few hardware resources as possible.
Once the model has been mapped, the inference happens only on the device, and not on the host CPU except for passing inputs and fetching outputs.
Performance measurement
Performance measures (FPS and power) are available for on-device inference.
Enabling power measurement is simply done by:
device.soc.power_measurement_enabled = True
After sending data for inference, performance measurements can be retrieved from the model statistics.
model_akida.forward(data)
print(model_akida.statistics)
An example of power and FPS measurements is given in the AkidaNet/ImageNet tutorial.
Command-line interface for model evaluation
In addition to the aforementioned APIs, the akida python package provides a command-line interface for mapping a model to the available device and sending data for inference so that hardware details can be retrieved.
akida run -h
usage: akida run [-h] -m MODEL [-i INPUT]
options:
-h, --help show this help message and exit
-m MODEL, --model MODEL The source model path
-i INPUT, --input INPUT Input image or a numpy array
Note
About the model statistics:
it shows the inference power/energy when measurable (i.e. whenever the inference is lasting long enough to collect meaningful data),
displayed numbers include the floor power.
the CLI output using a pretrained DS-CNN model and a random input
the CLI output using a pretrained AkidaNet model and a 10 images input
wget https://data.brainchip.com/models/AkidaV1/ds_cnn/ds_cnn_kws_i8_w4_a4_laq1.h5
CNN2SNN_TARGET_AKIDA_VERSION=v1 cnn2snn convert -m ds_cnn_kws_i8_w4_a4_laq1.h5
akida run -m ds_cnn_kws_i8_w4_a4_laq1.fbz
Model Summary # Summary with NP units allocation
___________________________________________________
Input shape Output shape Sequences Layers NPs
===================================================
[49, 10, 1] [1, 1, 33] 1 6 65
___________________________________________________
____________________________________________________________
Layer (type) Output shape Kernel shape NPs
===== HW/conv_0-dense_5 (Hardware) - size: 88748 bytes =====
conv_0 (InputConv.) [25, 5, 64] (5, 5, 1, 64) N/A
____________________________________________________________
separable_1 (Sep.Conv.) [25, 5, 64] (3, 3, 64, 1) 16
____________________________________________________________
(1, 1, 64, 64)
____________________________________________________________
separable_2 (Sep.Conv.) [25, 5, 64] (3, 3, 64, 1) 16
____________________________________________________________
(1, 1, 64, 64)
____________________________________________________________
separable_3 (Sep.Conv.) [25, 5, 64] (3, 3, 64, 1) 16
____________________________________________________________
(1, 1, 64, 64)
____________________________________________________________
separable_4 (Sep.Conv.) [1, 1, 64] (3, 3, 64, 1) 16
____________________________________________________________
(1, 1, 64, 64)
____________________________________________________________
dense_5 (Fully.) [1, 1, 33] (1, 1, 64, 33) 1
____________________________________________________________
No input provided, using random data.
Floor power (mW): 914.03 # Reference board floor power
Average framerate = 62.50 fps # Model statistics
Model metrics: # Model metrics:
inference_frames: 1 # - number of frames sent for inference
inference_clk: 93965 # - number of hardware clocks used for inference
program_clk: 152396 # - number of hardware clocks used for model programming
wget https://data.brainchip.com/models/AkidaV1/akidanet/akidanet_imagenet_224_alpha_50_iq8_wq4_aq4.h5
wget https://data.brainchip.com/dataset-mirror/imagenet_like/imagenet_like.npy
CNN2SNN_TARGET_AKIDA_VERSION=v1 cnn2snn convert -m akidanet_imagenet_224_alpha_50_iq8_wq4_aq4.h5
akida run -m akidanet_imagenet_224_alpha_50_iq8_wq4_aq4.fbz -i imagenet_like.npy
Model Summary # Summary with NP units allocation
_____________________________________________________
Input shape Output shape Sequences Layers NPs
=====================================================
[224, 224, 3] [1, 1, 1000] 1 15 68
_____________________________________________________
__________________________________________________________________
Layer (type) Output shape Kernel shape NPs
====== HW/conv_0-classifier (Hardware) - size: 1361244 bytes =====
conv_0 (InputConv.) [112, 112, 16] (3, 3, 3, 16) N/A
__________________________________________________________________
conv_1 (Conv.) [112, 112, 32] (3, 3, 16, 32) 4
__________________________________________________________________
conv_2 (Conv.) [56, 56, 64] (3, 3, 32, 64) 6
__________________________________________________________________
conv_3 (Conv.) [56, 56, 64] (3, 3, 64, 64) 3
__________________________________________________________________
separable_4 (Sep.Conv.) [28, 28, 128] (3, 3, 64, 1) 6
__________________________________________________________________
(1, 1, 64, 128)
__________________________________________________________________
separable_5 (Sep.Conv.) [28, 28, 128] (3, 3, 128, 1) 4
__________________________________________________________________
(1, 1, 128, 128)
__________________________________________________________________
separable_6 (Sep.Conv.) [14, 14, 256] (3, 3, 128, 1) 8
__________________________________________________________________
(1, 1, 128, 256)
__________________________________________________________________
separable_7 (Sep.Conv.) [14, 14, 256] (3, 3, 256, 1) 4
__________________________________________________________________
(1, 1, 256, 256)
__________________________________________________________________
separable_8 (Sep.Conv.) [14, 14, 256] (3, 3, 256, 1) 4
__________________________________________________________________
(1, 1, 256, 256)
__________________________________________________________________
separable_9 (Sep.Conv.) [14, 14, 256] (3, 3, 256, 1) 4
__________________________________________________________________
(1, 1, 256, 256)
__________________________________________________________________
separable_10 (Sep.Conv.) [14, 14, 256] (3, 3, 256, 1) 4
__________________________________________________________________
(1, 1, 256, 256)
__________________________________________________________________
separable_11 (Sep.Conv.) [14, 14, 256] (3, 3, 256, 1) 4
__________________________________________________________________
(1, 1, 256, 256)
__________________________________________________________________
separable_12 (Sep.Conv.) [7, 7, 512] (3, 3, 256, 1) 8
__________________________________________________________________
(1, 1, 256, 512)
__________________________________________________________________
separable_13 (Sep.Conv.) [1, 1, 512] (3, 3, 512, 1) 8
__________________________________________________________________
(1, 1, 512, 512)
__________________________________________________________________
classifier (Fully.) [1, 1, 1000] (1, 1, 512, 1000) 1
__________________________________________________________________
Floor power (mW): 912.23 # Reference board floor power
Average framerate = 43.48 fps # Model statistics
Last inference power range (mW): Avg 1021.00 / Min 925.00 / Max 1117.00 / Std 135.76
Last inference energy consumed (mJ/frame): 23.48
Model metrics: # Model metrics:
inference_frames: 10 # - number of frames sent for inference
inference_clk: 43000636 # - number of hardware clocks used for inference
program_clk: 998079 # - number of hardware clocks used for model programming
Using Akida Edge learning
Akida Edge learning is a unique feature of the Akida IP, whereby a classifier layer is enabled for ongoing (“continual”) learning in the on-device setting, allowing the addition of new classes in the wild. As with any transfer learning or domain adaptation task, best results will be obtained if the Akida Edge layer is added as the final layer of a standard pretrained CNN backbone. An unusual aspect is that the backbone needs an extra layer added and trained, to generate binary inputs to the Edge layer.
In this mode, an Akida Layer will typically be compiled with specific learning parameters and then undergo a period of feed-forward unsupervised or semi-supervised training by letting it process inputs generated by previous layers from a relevant dataset.
Once a layer has been compiled, new learning episodes can be resumed at any time, even after the model has been saved and reloaded.
Learning constraints
Only the last layer of a model can be trained with Akida Edge Learning and must fulfill the following constraints:
must be of type FullyConnected,
must have binary weight,
must receive binary inputs.
Note
a FullyConnected layer can only be added to a model defined using Akida 1.0 layers
it is only possible to obtain a FullyConnected layer from conversion when target version is set to AkidaVersion.v1
Compiling a layer
For a layer to learn using Akida Edge Learning, it must first be compiled using
the Model .compile method.
There is only one optimizer available for the compile method which is AkidaUnsupervised and it offers the following learning parameters that can be specified when compiling a layer:
num_weights: integer value which defines the number of connections for each neuron and is constant across neurons. When determining a value fornum_weightsnote that the total number of available connections for a Convolutional layer is not set by the dimensions of the input to the layer, but by the dimensions of the kernel. Total connections =kernel_sizexnum_features, wherenum_featuresis typically thefiltersorunitsof the preceding layer.num_weightsshould be much smaller than this value – not more than half, and often much less.[optional]
num_classes: integer value, representing the number of classes in the dataset. Defining this value sets the learning to a ‘labeled’ mode, when the layer is initialized. The neurons are divided into groups of equal size, one for each input data class. When an input packet is sent with a label included, only the neurons corresponding to that input class are allowed to learn.[optional]
initial_plasticity: floating point value, range 0–1 inclusive (defaults to 1). It defines the initial plasticity of each neuron’s connections or how easily the weights will change when learning occurs; similar in some ways to a learning rate. Typically, this can be set to 1, especially if the model is initialized with random weights. Plasticity can only decrease over time, never increase; if set to 0 learning will never occur in the model.[optional]
min_plasticity: floating point value, range 0–1 inclusive (defaults to 0.1). It defines the minimum level to which plasticity will decay.[optional]
plasticity_decay: floating point value, range 0–1 inclusive (defaults to 0.25). It defines the decay of plasticity with each learning step, relative to theinitial_plasticity.[optional]
learning_competition: floating point value, range 0–1 inclusive (defaults to 0). It controls competition between neurons. This is a rather subtle parameter since there is always substantial competition in learning between neurons. This parameter controls the competition from neurons that have already learned – when set to zero, a neuron that has already learned a given feature will not prevent other neurons from learning similar features. Aslearning_competitionincreases such neurons will exert more competition. This parameter can, however, have serious unintended consequences for learning stability; we recommend that it should be kept low, and probably never exceed 0.5.
The only mandatory parameter is the number of active (non-zero) connections that
each of the layer neurons has with the previous layer, expressed as the number
of active weights for each neuron.
Optimizing this value is key to achieving high accuracy in the Akida NSoC. Broadly speaking, the number of weights should be related to the number of events expected to compose the items’ or item’s sub-features of interest.
Tips to set Akida learning parameters are detailed in the dedicated example.